理实融合，课程融通——完全学分制下

   “人工智能数学基础”的教学探

            徐 博 杜宝珠 苏 婷 王咸鹏

                 （海南大学信息与通信工程学院，海口 570228 ）

摘要  针对完全学分制背景下“人工智能数学基础”课程面临的如何有效关联数学基础知识与实际工程问题，本文提出“理实融合，课程融通”教学思想及“兴趣启发-项目进阶-AI 陪练-课堂竞赛”的教学模式， 并结合多种评价机制保证课程目标达成情况。课程改革实践表明，学生表现优异， 课程目标平均得分 3.61，远超毕业达标标准（ 3 分），课程及格率达 93%。教学的满意度调查显示， 100%的学生对课程内容设计表示认可，表明课程的考核体系全面有效； 92%的学生认为课程模式提升了学习效率。

关键词：完全学分制；人工智能数学基础；教学改革；人工智能素养

Integrating theory and practice, harmonizing courses

—exploration of “foundations of mathematics for artificial intelligence”

under the full credit system

XU Bo    DU Baozhu    SU Ting WANG Xianpeng

(School of Information and Communication Engineering, Hainan University, Haikou     570228)

Abstract In the context of a full credit system, the course Foundations of Mathematics for Artificial Intelligence faces the challenge of linking foundational mathematical knowledge to real-world engineering problems.  This  paper  introduces  the  teaching  philosophy  of  “integration  of theory  and practice” and the model of “interest inspiration-project progression-AI coaching-classroom competition”, supported by diverse evaluation mechanisms to ensure course objectives are met. Curriculum reform has led to excellent student performance, with an average score of 3.61, far surpassing the 3-point graduation benchmark, and a 93% pass rate. Surveys show that  100%  of students appreciate the course content design and its comprehensive assessment system. Additionally, 92% believe the course model significantly enhanced their learning efficiency.

Keywords：full  credit  system;  foundations  of  mathematics  for artificial intelligence; teaching reform; artificial intelligence literacy

0 引言

人工智能（artificial intelligence, AI）源于计算机科学、数学、语言学、信息学等多领域的交叉与融合[1-2]。优秀的人工智能人才需要具备扎实的数学基础、强大的实践能力和全面的专业知识[3-4]。

完全学分制打破了学年学分制的时间与内容限制，赋予学生更大的学习自主权。近年来，国内多所高校推行完全学分制改革， 以服务国家战略、社

会需求，助力学生个性化成长[5-6]。然而， 在完全学分制的背景下，“人工智能数学基础”课程教学面临挑战：一是学生数学基础与学习进度不一，课堂教学难统一；二是课程内容的广度和深度难平衡， 难以兼顾不同层次学生需求。

此外，部分学生自主学习能力不足，学习精力分配失衡；理论与实践脱节，学生不明数学实用意义；传统考核无法全面衡量学生能力，亟待优化。鉴于此，本文围绕数学知识与人工智能实践的有效关联，提出“理实融合， 课程融通”理念，探索完全学分制下该课程的教学改革之路。

海南省高等学校科学研究项目“《人工智能数学基础》课程建设研究与实践探索 ”（Hnjg2024ZD-2） 海南省高等学校教育教学改革研究项目“专业学位研究生产教融合育人模式研究 ”（Hnjg2023ZD-16）

1 课程教学改革背景

在完全学分制背景下，“人工智能数学基础”课程的重构围绕毕业要求，制定了四个关键课程目标。课程目标与毕业要求如图 1 所示。其中，对于课程目标 1 、2 、3  都支撑毕业要求 1（工程知识）的情况：课程目标 1 的工程知识侧重于学习基本概念、基本原理和基本方法；课程目标 2 的工程知识侧重于掌握数学建模和算法分析的知识； 而课程目标 3的工程知识旨在理解数学知识与人工智能方法之间的联系。

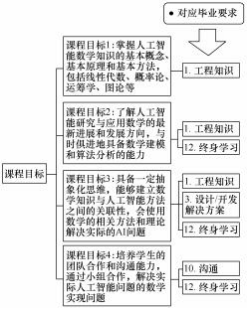
图 1 课程目标与毕业要求

然而，如何有效关联数学基础知识与实际工程问题仍是一个主要挑战。当下，诸多教学改革试图解决数学基础与实际应用脱节的问题。例如，项目驱动教学[7] 常见却未考量学生层次差异，难以适配完全学分制；以赛促教[8] 虽于竞赛有成效，但赛制繁杂、获奖难，学生成就感低，难激发持久兴趣；翻转课堂以学生为中心[9-10] ，兼顾个体差异能提升自主学习能力，但在课程目标达成评估方面有所欠缺；还有“剧本杀”“密室逃脱”等创新课堂设计[11]，虽能提升参与度，却不利于学生线下自主学习。

2      “人工智能数学基础”课程改革体系构建与实施

在完全学分制背景下，针对数学基础知识与实际问题有效关联的主要挑战，本课程在课堂中实施“兴趣启发-项目进阶-AI 陪练-课堂竞赛”的教学模式。通过将课堂教学任务与学生学习情况结合， 支撑形成性评价，实现目标达成情况的评估[12-13]。

为更好地实施该模式，课程重新设置教学内容，最后提出多元考核评价体系，对教学效果进行整体性评价[14] 。该模式能够满足完全学分制下学生全面发展和个性化发展的要求，增强了课堂参与感和即时成就感。课程教学模式设计如图 2 所示。

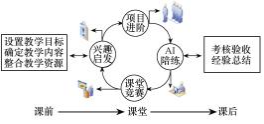
图 2 课程教学模式设计

2.1    课前：“人工智能数学基础”专职教师团队以“兴趣启发、逐步进阶”原则优化教学内容

1）培养“人工智能数学基础”的专职教师

人工智能教师应该与数学专业教师合作开展研究，不仅要在讲授基础数学课程时具备扎实的知识储备，还要在科研和案例教学方面下功夫，以确保数学教学能够有效服务于专业学习。

授课教师团队兼顾知识传授、能力培养与素质提升，对课程难度予以调整。如讲特征值和特征向量时引入主成分分析（principal component analysis, PCA）在 Eigenface 人脸识别中的应用[15]，讲解链式法则结合反向传播神经网络算法阐释其在手写数字识别中的作用。这些实例向学生直观展现数学理论与人工智能实践的紧密关联，有力促进数学基础课与人工智能专业课的衔接。

2）遵循“兴趣启发”和“逐步进阶”原则

授课教师基于“兴趣启发”与“逐步进阶”的原则，提前规划本学期教学内容。课堂融入数学通识教育，关联数学、人文与社会问题，循序渐进地结合人工智能理论与实际应用[16-17]。先以趣味示例、文化启示拓宽学生视野， 激发其学习兴趣；接着逐步进阶，依章节融入实际案例，让知识与应用协同推进。实践案例不仅应贴合数学课程内容，还需要充分考虑学生的知识结构和实践能力。若授课对象为大一学生 ，鉴于其编 程能力弱， 实践项目选用Python 或 R 等易上手语言，避开未掌握的 C 程序设计语言。

这些创新做法有效地解决了原本课程中可能存在的“枯燥”和“理论与实践脱节”的问题，在课程内容设计上做到了“理实融合，课程融通 ”。

2.2    课堂：执行“兴趣启发-项目进阶-AI 陪练-课堂竞赛”教学模式

本教学模式将课堂教学任务中学生的学习情况用于支撑形成性评价，帮助不同学生找到适合的学习路径，并结合该模式下的成果进行课程目标达成情况评估。课程目标 1 、2 、3 、4 达成情况评估方法见表 1。以课程目标 3 为例，其评分内容涵盖在项目进阶和课堂竞赛中展示的抽象化思维能力，以及运用数学方法和理论解决实际人工智能问题的能力，还包括领导团队协作，通过编程实现模型， 且解决方案表现出色的能力。这些评分内容与毕业要求 1（工程知识）、3（设计/开发解决方案）和 12（终身学习）相对应。通过这些内容，可以对课程目标3 的达成情况进行 1～5 分的评估打分。

表 1 课程目标达成情况评估方法

在该模式下，对每个学生进行课程目标达成情况评估，最后对每个课程目标完成情况的等级人数进行统计，得到总体课程目标达成情况的分值评估。

下面以“概率论、贝叶斯理论及其在 AI 中的应用”这一知识点的讲解过程为例，具体介绍这一教学模式各个环节的实施方法[18]。

1）兴趣启发

课程初期，教师先简要介绍贝叶斯定理基本概念，重点讲解如何用先验概率结合新数据更新后验概率，帮助学生理解这一过程在决策中的重要性。同时，教师展示贝叶斯定理在疫情预测、金融风险评估和推荐系统等领域的实际应用。通过该教学过程，这些实例有效激发了学生对贝叶斯定理的兴趣。

2）项目进阶

课程步入项目进阶阶段后，学生分组开展与知识点相关的小型项目。教师提供实际数据集，助力学生将知识用于真实场景，具体步骤如图 3 所示。学生在实践中加深对理论的理解，提升数据处理、编程与模型构建技能。而且， 小组合作模式培养了团队协作、沟通及解决实际问题的能力。

3）AI 陪练

在 AI 陪练阶段，课程将聊天生成预训练变换器（chat generative pre-trained transformer, ChatGPT）和 Canvas 平台结合， 增强学生的学习体验。 AI  陪练环节实施过程和方法如图 4 所示。AI 陪练不仅提高了学生的自主学习能力，还促进了知识的深度理解和应用，解决了传统教学中“学习-应用”之间的脱节问题。

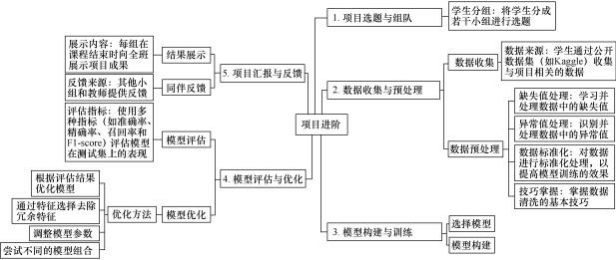
图 3    概率论和贝叶斯理论的项目进阶

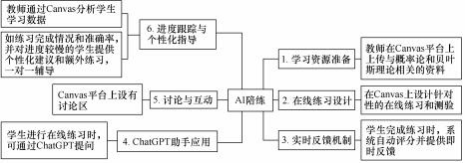
图 4 概率论和贝叶斯理论的 AI 陪练

4）课堂竞赛

在知识点教授尾段设课堂竞赛， 如图 5 所示。例如， 围绕概率论与贝叶斯理论应用，各小组分析AI 案例数据、进行预测并展示方案，将理论转为实操技能。此外，经过课堂竞赛的推动，学生们的学习兴趣被进一步激发，对后续学习展现出更加高涨的热情。至此，一个包含“兴趣启发、项目进阶、 AI 陪练、课堂竞赛”四个环节的闭环教学模式得以形成。

该模式紧密联结基础数学与实际问题，提升学习兴趣与应用能力，助力高质量达成课程目标， 为学习、职业发展筑牢根基。

最终成绩通过综合加权系统评定，涵盖团队评估（35%）、个人期末评估（40%）及日常表现（25%）。团队评估包括学期中团队考核、项目进阶及课堂竞赛成绩；日常表现基于课堂、出勤、线上学习和课后检测情况。基于这种多元考核最终可以得到每位学生的总结性评价，有助于系统地评估学习成果和学习目标达成情况。该创新性评价方式更为准确地衡量了学生的综合素质和实践技能， 充分发挥了评价在教学过程中的积极作用。

2.3    课后：科学运用考核手段，构建线上与线下一体化的多元考核评价模式

本轮课程教学改革采用多元化、多频次的考核机制[19] ，分为学期前、学期中和学期末，涵盖单人及团队考核。多元考核评价模式如图 6 所示，学期前考核通过线上问卷调查进行，采用诊断性评价，对学生知识结构进行摸底。学期中考核采取团队形式，教师提前发布课堂内容相关科技论文，学生自主选题、组队。考核依据报告的完整性、准确性、创新性及汇报的专业素养（各占 25%）进行综合评分。借此，教师能了解学生前期学习状况，助力学生回顾知识、开展案例应用。学期末考核为个人卷面考试，考查学生对课程知识的掌握与应用。教师通过考核结果总结教学重难点，为后续课程改进提供依据。此外，教学模式依托 Canvas 平台对学生自主学习进行跟踪、监控、评估和反馈。教师通过平台设置“作业”“测验”“讨论”“评分”等模块。学生则可在平台上预习材料、参与讨论、学习在线课程，并完成同伴评价和小组互评。

图 5    概率论和贝叶斯理论的课堂竞赛

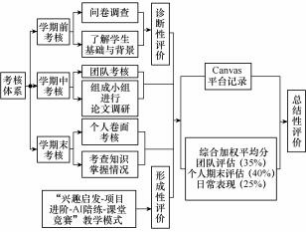
图 6 多元考核评价模式

3 教学效果

本课程面向 140 余名学生推行“兴趣启发-项目进阶-AI 陪练-课堂竞赛”教学模式，结合多元考核评价，成效显著。及格率达 93%，各项课程目标均达预期，学生于工程知识、设计开发方面表现突出，课程目标平均得分 3.61，超过达标标准（3 分）[20]。课程目标评价见表 2。未及格学生主要表现为数学基础与思辨能力薄弱，在关键问题理解、基本计算尤其是矩阵运算方面有欠缺。后续将强化学生思辨引导与基本计算训练。

表 2 课程目标评价